伊原康隆＞＞＞藤原辰史

　
　藤原さんの懐の深さにも感銘を受けつつ今回も印象深く拝読いたしました。歴史学における教育上の具体的なご提案にも非常に興味を感じました。数学分野との比較をいろいろ思い起こし、再吟味してから改めてご質問したいと思います。

習、探、能の心理面のバランスは？

　
　今回は予告のように

「〇〇しなくてはならない」「〇〇したい」「〇〇できる」

について、主に心理面から考えるスタートを切りたいと思っております。さしあたり糸口だけですから今後どんどん突っ込んでください。まず、これら三要素とその区別をはっきり意識し「対等に重要な要素」とみなしましょう。その上でそれらの間の相互作用を心理面から探ってみたい。でもまずは適切な用語の吟味と選択でしょう。ところが日本語での適切で簡単な用語が、私には容易に見出せないのです。そのわけが、歌への興味から少々勉強したイタリア語の文法から、あるとき、分かったぞという気がしました。

　日本語では上記の表現のように 〇〇 が先行するので、〇〇 モニャモニャになってしまいがちで、「自分のためにこそ、そのモニャモニャをはっきりさせることが重要だ」という意識を伝統的に持ちにくいのではないか、と。対してイタリア語では語順が逆で、構文は

D 〇〇　 V 〇〇　 P 〇〇

となり、先行する D, V, P はそれぞれ「しなくてはならない」「したい」「できる」にあたる「動詞」です。この語順はイタリア語に限りませんが、イタリア語では D, V, P は重要な「三つの特殊な動詞」として文法的にも特別な地位を与えられています。従属動詞と訳されていますが、従属するほうではなく、させる方です。それによってまず「ならない」「したい」「できる」を唱える、そして直後に 〇〇 が続きますがこれも動詞の不定形です。会話では控えめがよいのはイタリア語でも同様で、D, V, P にも条件法など婉曲表現形が使われはしますが、自分の心情がどこにあるかの自意識の区別はくっきりしていると思います。

　D, V, P の不定形はそれぞれ dovere, volere, potere で、デューティー、ボランティア、ポテンシャルと通じています。「行きたい」は volere の条件法の vorrei を使って ''vorrei andare'' など。なお「できる」には 「知っている」に通じる sapere （ホモ・サピエンスのサピ）もあり、習得した知識や技能などに使われますが、こちらはやや静的ですので、ここではより動的でポテンシャルとも繋がる potere に代表してもらうことにします。どうやらイタリア語文化圏では、これらの相互関係とバランスを意識する機会が我々より多いのではないかと感じます。とにかく自らの行動の指針を考える際、これら三つの動詞は普遍的なキーワードではないでしょうか。学びにおける「習と探」で考えを整理する際にも D, V, P を三方向の力とみなすと考えやすくなるのではないか。

　それぞれを細分化してみましょう。すると D は細分化された具体的な課題、P はそれが求められる時間内に出来るか、になる。他方 V は最初は「夢」と言われるぐらい無限遠方にある、とはいえ D や Pと連携するには V も細分化されていないと力を発揮し難い。V の目標を段階分けし細分化してそのときどきの自らの課題 Dとなす。知恵のしぼりどころでしょう。逆に D であったのがあるきっかけによって「V -スイッチオン」になるなど、入れ替わりや融合もあるわけです。この3つがバランスよく成長しながら生きていければ理想的ですが、なかなかそうは......。学校時代の主な D は、本来は生徒の P を伸ばすためのプログラムですが、個人差があるため個人個人の P の成長とは繋がりにくい部分を抱えていますね。そこに生徒側から新たな V が生じるのでしょう。

　そして常識路線は「D の意向に沿った P の成長を努力目標にとり、それに従ってD と Vを調整せよ」ではないでしょうか。私は、むしろ 「 V の（根を深める）成長 」を主眼にしたらどうか、と思っています。「イタリア的情熱を日本的に多少コントロールして」かな。まず初期の V。これは当初の強い憧れであっても自分の P とはマッチしないことが追い追い分かってくるかもしれない。それでも初一念を貫徹しようとする美学はちょっと狭すぎて危険なようです。むしろ D と P のせめぎ合いの中で V 自体の根の行先を調整しながら到達するのが本当の V ではないのかな？　

　さて前回、理系における感性の話をいたしました。数学の具体例は？　いやー、若い頃に研究者の卵として在米中パーティーで一般のご婦人から話しかけられたときを思い出します。

「何をしているのか？」　　（小さな声で）「マセマティックス」
「オー、マーセメアティックス」（「ア」にアクセント、笑顔ながら額をしかめて）

「数学は大の苦手、でも数学者はかわいいところもあるから数学の話さえしなければOKよ」という雰囲気。でも今は仕方がありません。藤原さんに問うていただきましたし、「理系での感性の話」の続きとして「AIに出来ることとの対照」の話題をいずれ取り上げなくては、と思っておりますので今日はその手始めを。

数学は自ずと広がる世界

　
　複素数の導入がその一つです。2次方程式の解法で習う「2乗して -1 になる仮想的な数 i 」。「何これ？　無いものをあるといいくるめる勝手な指導者の教え？」 いや、違います。最初の動機はともあれ、「直線状の数しか見えていなかった人類が平面状の数も見えるようになった」というのが正しい解釈だったのです。まずメモリをつけた直線上の点であらわされる実数の範囲で「-1 倍は方向の180°反転」というのはよいでしょう。では平面上で考えて「（たとえば）左に 90°回転 」はどうでしょうか。「左向け左！」を 2 回繰り返すと「後ろー、向け！」と同じですから、もしこの動作を新しい数 i で表し「2つの動作の連動」を「対応する数たちの積」で表せるのなら、この場合 i の2乗は -1 になるでしょう。そうです。虚数単位と呼ばれる数 ± i は（その符号に応じて左右への）90°回転だったのです。数学者の合宿での左向け左は「アイをー掛けろ！」、かどうかは知りませんが。大切なのはこの

「数は直線」思考から「平面思考での新しい数」

への発想転換です。回転の角度は直角とは限りません。より一般の複素数を考えれば一緒に扱えます。複素数は2つの実数 a, b と文字 i を用いて形式的に a + bi と表せる数のことです。これらに和、差、積を、普通の演算の規則で、ただし等式 i² = -1 をあわせて、定めたものです。b = 0 のものを実数 a と同一視し 0 + 0i を複素数としての 0 と思えば、0 以外の数による割り算もできます。そして幾何と結びつけるため「複素平面」という言葉も導入されました。それは平面に
(x, y) 座標系を入れ、点(a, b) は複素数 a + bi と対応させるのです。x 軸は実数部分、y 軸は純虚数（bi 型の数）部分です。0でない複素数のもう一つの極座標表示は、正の実数 Rと角度 t を用いた表示

z = R(cos t + i sin t) 　　　・・・（1）

です。R は原点からの距離、 t は原点からこの数に向かう直線を x 軸の正の方向からみた角度です。角度は今後のため弧度法を用いることにしましょう。

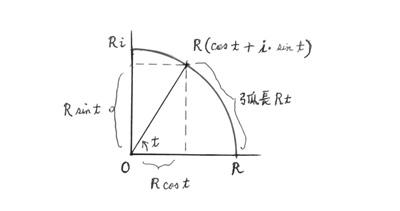
　極座標表示によって複素数の積の幾何的意味が明瞭になります。(1) において R, t に ' をつけた数を z' で表すと、 z と z' の積は

zz' = RR' (cos (t + t') + i sin (t + t'))

で与えられます（三角関数の加法定理そのものです）。積の距離は距離の積、積の角度は角度の和という関係です。特に「 i を掛ける」は原点から見て「左に直角に回転」、また任意の n=1,2,3, ......に対して

　　　 　　zⁿ = Rⁿ (cos (nt) + i sin (nt)) 　　(n = 1,2,......)

が導かれ、これは今日の最後の話とつながります。

（幾何と代数）　複素数は代数、解析、幾何を結ぶ重要な対象です。その中で数学以外の分野の方々にも垣間見ていただきたいのは特に解析的側面なのですが、今回は（ここまでの話と直結した）代数がらみの「さわり」だけにいたしましょう。上の公式から方程式 zⁿ = 1 の複素数解は、

ζ = cos (2π /n) + i sin (2π /n)

と置くとき 1, ζ , ζ², ......, ζ^n-1 で、これらは単位円周を n 等分する複素数であることが容易に分かります。幾何学における正 n 角形の作図問題と代数学における方程式 zⁿ = 1 の根の問題とがこのように対応しているのです。下の図は n = 5 の場合です。

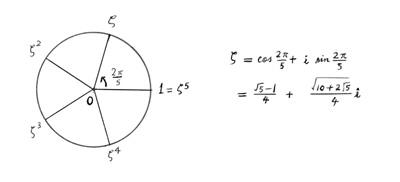
これを具体的に活用し従来知られていなかった正多角形の（定規とコンパスによる）作図可能性を指摘して一躍有名になったのが若い頃のガウスでした。たとえば多項式 z¹⁷-1 を z-1 で割ると
16次多項式になり、それを解くには（16 = 2⁴だから n = 5 の場合と同様に）2次方程式を（この場合は）4回解けばよく、結局平方根をとる操作だけで解が求まる。だから正17角形は作図可能。逆にn が素数で n-1 が 2の冪でないときは（定規とコンパスだけによる）作図は不能ということも証明されました。ポイントはその手法自体の普遍性にあります。幾何と代数の上記の関連性、それに加えて、方程式を研究するには（この場合 n 個ある）根たちの間の関連性を知ることが有用だ、という認識です。この方向を深く開拓したのは19世紀前半のアーベルやガロアでした。

　代数面での複素数の役割についてもう一つ追加しますと、

定数でない任意の多項式 f (z) に対し、方程式 f (z) = 0 は根をもつ

という代数学の基本定理（ガウス）があります。多項式の係数は複素数でも構いません。これこれには根がないからまた広げる、といった必要はないことが分かりました。そしてこの証明も複素数の微積分を使えば実に簡単です。「解を探す」のではありません。アイディアは、仮にそうでないとすると 1/ f (z) は複素平面全体の上の関数として「あまりにも都合が良すぎる性質をもってしまうから」というだけです。

　対象の枠の自然な広げかたに気づき、その視野で関連性を見る、これこそ「AIにはできない」人知でしょう。この話にもまた戻ってきたいと思います。

　藤原さんの前便へのリスポンスには残念ながら吟味時間不十分でしたが、引き続きどうぞよろしくお願いいたします。

• Tweet
•