伊原康隆＞＞＞藤原辰史

　新緑のころの藤原さんからのご書簡で「円に関して何かを」とのご要望をいただきました。夏休みの学生達を安価に泊めてくれていた山寺、畳の大部屋、それぞれ勉強に疲れるとやってきて輪がうまってくる「車座」、そこでの「何か」の共有、懐かしい思い出が多々ありますが、どうも収束しにくい。そこで今回は六月の「一葉」として、目線の変化と複素解析関数の話にいたしましょう。

　歩み方向と目線方向のずれは、現実と理想のずれからも生じるでしょうから、それがどういう周回運動をつくるかは、人の思いと行動に関する問いでもあると思います。そこで複素解析関数が登場する仕組み、それと対応して時間軸にも虚数を導入すると視界がどう開けるか。こんな話をお聞きください。

　なお、数学的補足は、数式に適したソフト"LaTeX"で別途作成したファイルとリンクでつないでいただけることになりました。どうぞご利用ください。

１　目線と行く先

　普通歩くときは目線を（基本的には）体の正面に向けて歩きますね。ここでちょっと空想してみて下さい。眼が一つしかなく、それが顔の正面からある角度（たとえば直角）偏ったところにあるとするのです。そして平面の上を

　「目線を特定のランドマークから動かさず顔の正面方向に歩き続ける」

と、どんな行路をたどるでしょうか？

　たとえば眼が正面の左直角方向にある場合、その答えは「ランドマークを中心とした円周を左回りに回る」ですね。数学の授業では「円の径と接線は直角に交わる」と教わるし、スケートで円を描くには「目線の角度が大切」とも遊びの中で教わりました。

　 一般の場合の定性的な答えは、目が真横より前方の場合は「回りながらランドマークにじりじり接近」、後方の場合は「回りながら限りなく遠ざかる」となります。これも大まかなスケッチを紙あるいは心に描いてみれば見当がつくでしょう。

２　連想される社会問題との関係は？

　これらが人間社会の問題と一体何の関わりがあるのか、想像をたくましくしてみましょう。まず、社会状況を表せそうな指標を数個選び、それらを座標とする空間の「点」によって（各集団の時々の）社会状況を大まかに表現できるものと仮定しましょう。そして時間軸をその空間に

　　　時間軸　→　社会状況の（一つの）表現空間

という対応で埋め込み、これを「運動」とみなすのです。「歴史は繰り返す」は、この運動がほぼ周期的に「どこかを回っている」ことでしょう。単純な動きの場合は「中心点」らしきものがあるかもしれませんね。ブランコの動き（実質1次元）にも中心があり、子供は大きく揺らしたがるが、生じたブレは中心に戻らせる力によってもとに戻り、さらに慣性によって今度は逆方向にブレる、この繰り返しですね。指標を1つでなく（まずは）2つにして平面で考えても、やはり何らかの中心点の存在を仮定してみたくなります。それは、格差最小の状況でしょうか。

　いずれにせよ、社会あるいは指導者が、現在進行中の方向（顔の正面）と理想とする方向（目線）が「違うぞ」と考えれば上のような動きになるのではないでしょうか。方向の相違が直角なら円を描き、それより狭ければ内側に入り込むように回り、広ければ回りながら遠ざかる。それらのゆらゆらが歴史が描く曲線ではないか。それにしても中心点、 目線、社会状況をなるべく簡潔に表せる2つの代表的指標 とは一体、何でしょう？

３　複素解析関数は角度を保つ写像

　1の問いを、広い観点から眺めやさしく解くには、複素解析関数が必要です。複素関数とは変数も値も複素数の関数のことですが、幾何的には複素平面から複素平面（筆者の2月分または補足(i)参照）への写像に他なりません。「関数」というと式を連想しますが「写像」ならそのイメージで理解したくなるでしょう。

　複素関数の理解はイメージから入るべきです。以下、変数が動く複素平面をC1、値が動く複素平面をC2、そして写像とみた関数を f と記します。

　　　f：C1　→　C2

この f が複素解析的（微分可能）とは、 感覚的には「親指と人差し指を好きなように広げて C1 の中に置くとき f はその形を変えないこと」、言い換えると「両指のなす角度も両指の長さの比も保たれる」という条件です。ただし、小さい小さい極限での話です。なお、これらが複素微分可能性と対応するわけは、分数に関する条件　b/a = b'/a' を言い換えると（複素数でも）b'/b = a'/a 、というごく簡単なことに過ぎません（補足(ii)参照）。

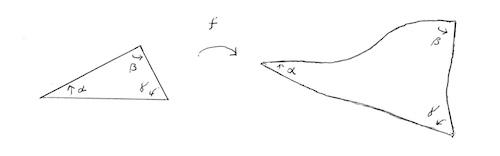
　実数関数では、微分可能性は「なめらか」というだけのありふれた条件で誰の関心もひきつけませんが、複素変数では「局所的な形を保つ」という非常に強い条件を含んでいます。実軸上のなめらかな関数を複素解析関数に延長できるかというと大抵はできないし、できる場合も一通りだけに限られます。

４　問題の見直しと発想の転換

　これらを踏まえて当初の問題に戻りましょう。平面は複素平面 C 、運動は時間軸 から C 内への埋め込み写像とみなします。運動中の瞬間速度をその位置 w から発する矢印で表します。矢印の向きと長さが瞬間速度の向きと大きさを表すのです。他方、ランドマークを原点 O に置くと、位置 w 自体も「 O からの距離と向き」を持っています（破線矢印）

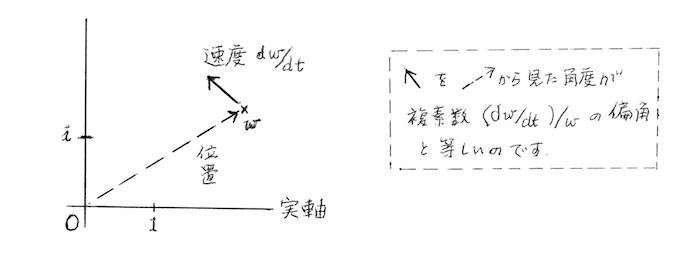
そして問いの条件は

　「速度の向きは、位置の向きと（たとえば）直角の差を保つ」

ということでした。それぞれの矢印を、以後はそれぞれと向きも大きさも等しい複素数によって表すのですが、二本の矢印の向きの差は対応する二つの複素数の比の偏角と等しいことを踏まえておいて下さい（補足(i)）。

　ここで、もう一つポイントがあります。ときどきの瞬間速度の「大きさ」は進む経路とは無関係でした。だから特別な場合として、それが O からの距離に常に等しい場合（従って近づく程スローダウン、遠ざかる程スピードアップ）に解けばよいわけで、実はそれが角度の制約との相性が最もよいのでした。

　速度は時間の微増に対する位置の微増の比ですから、通常 dw/dt と表示します。次に破線の矢印は w そのものですから、速度に関する問題の条件は、dw/dt と w との複素数としての比が「偏角 π/2 で長さ 1の複素数、つまり虚数単位 i 」と言い換えられます。式では

　　　dw/dt = iw 　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・　(1)

と、ごく簡単になりました。

　ここで発想を転換します。もし時間軸を広げて虚数 i に対して　z = t i とおけば上の方程式は

　　　dw/dz = w 　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・　(2)

となり、これは指数関数 w = e^z が満たす方程式と同じではないか！　それなら e^ti が問いの（直角の場合）の答えとなり、さらに、i の代わりに長さ1で与えられた偏角を持つ他の複素数 ζ をもってくれば　e^ζt が一般の場合の答えではないか？　後の見るように、正にその通りなのです。

５　指数関数の２つの顔

　方程式(2)、 即ち dw/dz = w を満たす複素解析関数 z → w は、定数倍を除いて唯一つで、初期条件 0 →1 によってその定数も定めたものが指数関数

　　　w = e^z

とよばれる基本的に重要（で素敵）な複素解析関数です。それは

　実軸に制限すると文字通りの指数関数になり
　虚軸に制限するとそれを単位円周に巻きつける周期関数になる

複素数まで考えてはじめて見られるこの統合性が、一つの方程式と複素微分可能性というだけから、すらすら導びかれます。

　たとえば、和を積に移すという著しい性質

　　　e^z+z' = e^ze^z' 　　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・　(3)

の証明もたったの二行 。「z' を固定して(3)の左辺を z の関数とみたものも(2)を満たす。だからそれは e^z の定数倍となり、その定数は z = 0 と置くことで e^z'と分かる」。

　上で予告した実軸上での振る舞いについては、まず f(1) = e によって定まる定数 e は ネイピア数または自然対数の底と呼ばれ、その値は e = 2.71828...です（補足(iii))。そして(3)から派生する e^nz = (e^z)ⁿ を、n が整数の場合、有理数の場合、連続性を使って実数の場合、と順次使えば、x が実数ならこの関数は e^x ( e の x 乗 ) 、従って右向きに急上昇であることが判明します。

　他方、虚軸{yi} 上で y が 0 から出発するときの w = e^yi は、方程式(2)そのものが「1から出発する w の進路は、O と w を結ぶ角度と直角で、速度の大きさは1」ということをむき出しで示していますから、虚軸を（Oを中心とする）単位円周に等長で巻きつけていきます。式で書くと

　　　e^yi = cos(y) + i sin(y) 　　　　　　　　　　　　　　　　　　　　　　　　・・・　(4)

特にy = 2πで一周して　e^2πi = 1 、従って(3)と合わせて一般に

　　　e^z+2πi = e^z （指数関数の周期性）　　　　　　　　　　　　　　　　　 　・・・　(5)

また任意のzに対する値も

　　　e^x+yi = e^x(cos(y) + i sin(y)) 　　　　　　　　　　　　　　　　　　　 　　 ・・・　(6)

によって定まります。

　写像 C1 → C2 としての関数 e^z のイメージを描いてみましょう。

　行く際は C2 から原点を除いた残りです。最初は「絨毯巻き」。まず C1 を絨毯と見て、上にぐるぐる巻いていきます。実軸など C1 の水平線は巻物の中でも直線として保たれ、垂直線はそれらと直交する半径 1 の円に重ねられます。次は「傘」に切り替え。左無限遠方を絞って傘の先端（石突き）とみなし、中棒を C2 の原点上に立ててから傘を開きます。その（無限に広い）傘布を C2 に落とす。すると C1 の水平線は（親骨などを経て）C2 の原点から発する放射線に、垂直線は原点を中心をした円周上に移される。これが写像 z → e^z のイメージです。

　歴史は急展開と周期性とを兼ね添えていますが、指数関数も同じ雰囲気を持っていること、そのわけは複素解析性という一つの法則にある、ということに多少興味を感じていただけたでしょうか。

　そして最初に述べた問題の一般の場合

　「眼が真左から角度 θ の位置にある場合の運動の軌跡」

（正面寄りを正とする）は、 O から 虚軸と角度 θ（左側が正）で斜め上方に伸びる半直線 の e^z による像になります。図（補足(iv)）は θ = ± π /30 の場合です。指数関数の逆関数である複素対数関数の自然な姿については補足(v)をご覧ください。

6　吟味と議論と期待

　まず個人の時間軸を何らかの心象風景の空間に埋め込んで考えてみると、自分の場合からの想像ですが、人それぞれの時間軸には僅かでも虚数が入り込んでいるのではないか？　その虚数部分とは、それまでの進行方向とそのとき心が向かっている方向の「角度のずれ」ではないか？　そんな気分がしないでもありません。「真っしぐらに一直線」では、どんどん加速して破綻するだろうから、生命現象としても、それを振り返り見直すための「幅」として虚数部分が必要ではないのか、ときには回る、直角回転を繰り返せば後ろ向きになる、とか......まあこんなことは「何とでもいえる」かと思いますが、もし体内時計の仕組みなどで説明できたら面白いでしょう。

　でも、今回の話で本当にお伝えしたかったのは、理系の研究の芯たる伝統です。「関連性」というものはできる限り一般化（すなわち抽象化）して捉えよう、そうすると奥にある法則性が見えてきて、人間の認識の幅も（それまで無意識領域だった方向に迄）広がり得る......。

　これはしかし単純化と切り離せず、単純化を敵と考えるのとは相容れない思想でしょう。でも単純化にも、区別が雑、ご都合主義的、等に加えて、深いところでの共通性から抽出された単純性もあるだろう。それらを一括排除するより、少しずつ「よりよい単純化」を構成して検討を重ねる、というのが科学が進んできた道でした。最初は幼稚な単純化から始まり批判を受けていたようですが。そうしないと別種の単純化を求めるようになるかもしれませんし。

　複雑性と単純化の狭間、これが残り少なくなった対談で私が徘徊したいと願っている主な場所です。広い意味の言語の問題とも切り離せないと思います。

　数学のように解が一つしかないものと世の中とは違う、とよくいわれました。もっともですが、まず「解が一つしかない」は、数学の「試験問題」との混同ではないでしょうか。数学自体では、解が存在し得ない問いもあれば、範囲を広げれば（ i = √-1 のように）解が存在する場合もあります。その場合「解」とよぶより「根」とよぶべきでしょう（「根気の根」！）。根は複数あるのが普通で、それらを見つけようと焦る前に「複数の根の間の関係性を把握しようとする」のが数学が歩んできた道です。それによって「根が解になり得るか否か」も見えてくるのでした（ガロア理論）。

　急がずに、個々の分からないものにも名前をつけ、分からないもの同士の間の関連性を研究するーーこれは時間がかかることで、世代にわたって引き継いでいかなくてはならないでしょう。今後もどうぞよろしくお願いします。

• Tweet
•